モンティ・ホール問題を考察するための３封筒問題

　私がモンティ・ホール問題を考察するときは、回答者の選択したドアＡが当たりのドアである確率を求めようとする（参照）が、【モンティ・ホール問題：補足２】で紹介した【Monty Hall 問題 － Lectures by Nakao Y】や【モンティホール問題のエクセレントな説明を見つけたんで紹介】で紹介されている解法は回答者が当たりのドアＡを選択した確率を求める。回答者の選択したドアＡが当たりのドアである確率を求める手法と回答者が当たりのドアＡを選択した確率を求める手法は言葉だけを見ると同じように感じるが、少し異なる。前者は「回答者が最初に選択したドアはＡ」と決めて解くのに対し、後者は「当たりのドアはＡ」と決めて解く。前者はＡ、Ｂ、Ｃの各ドアが当たりである確率を変えて応用問題を作ることができるが、後者はＡ、Ｂ、Ｃの各ドアが当たりである確率ではなく、回答者がＡ、Ｂ、Ｃの各ドアを選択する確率を変えて応用問題を作る。前者の方が変形３囚人問題（参照）に近い応用問題を作れる。
　前者と後者で共通していることもある。それは、回答者が選んだドアにしろ当たりのドアにしろ、一つに決めて解いていることである。もしも前者で回答者が最初に選択したドアを不明にして、後者で当たりのドアを不明にして考察したらどうなるだろうか。モンティ・ホール問題では司会者の開けたドアが判明した状態と判明していない状態とでは解法が異なった。さらに不明なことを増やしたら解法はどうなるだろうか。

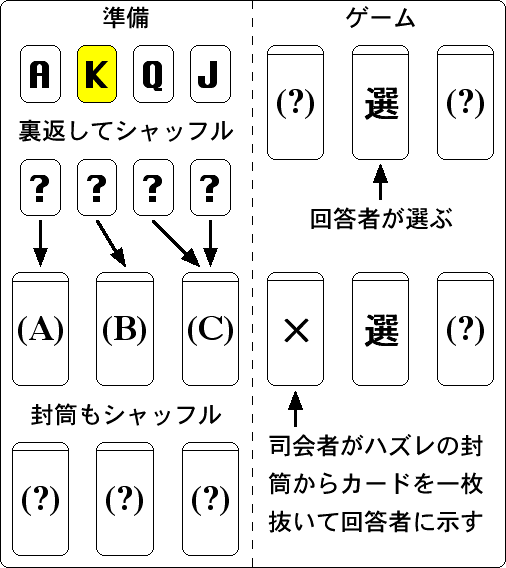
　そこで、次のような問題（ゲーム）について考察してみる。

1. 裏が同じで表が異なる４枚のカードを用意して、１枚を「当たり」と決める。例えば、トランプでエース（Ａ）、キング（Ｋ）、クイーン（Ｑ）、ジャック（Ｊ）を用意して、キング（Ｋ）を当たりと決める。
2. カードを裏返して位置が分からなくなるようにシャッフルする。
3. 表に（Ａ）、（Ｂ）、（Ｃ）と書かれた３枚の封筒を用意し、４枚のカードを裏返したまま（Ａ）に１枚、（Ｂ）に１枚、（Ｃ）に２枚入れる。これで、当たりのカードが入っている確率は（Ａ）が 1/4、（Ｂ）が 1/4、（Ｃ）が 1/2 になる。
4. 封筒も裏返して位置が分からなくなるようにシャッフルする。
5. その状態で回答者に３枚の封筒のうち当たりのカードが入っていると思われる封筒を選んでもらう。
6. 回答者が選ばなかった２枚の封筒のうち当たりのカードが入っていない封筒から１枚、司会者が抜き出して回答者に見せる。
7. 最初に選んだ封筒と司会者がカードを抜いて示さなかった封筒の２枚の封筒から、回答者が選択し直す。

　回答者が最初に選んだ封筒に当たりのカードが入っているのなら選択を変えない方が良くて、回答者が最初に選んだ封筒に当たりのカードが入っていないのなら選択を変えた方が良い。そこで、回答者が最初に選んだ封筒に当たりのカードが入っている確率を求めることになる。

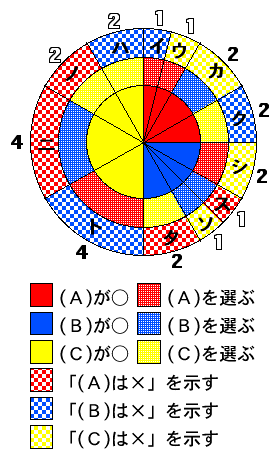
　確率を求める際に役立つように次の図を用意した。

　１周360度が確率１で、面積（角度）の比が確率の比である。計算しやすくするために、各領域の外側に面積の比を書いてある。当たりの所は白抜きにしてある。
　例えば、次のように見る。

• （Ａ）が当たりの確率は(イ+ウ+カ+ク)/(イ+ウ+カ+ク+シ+ス+ソ+タ+ト+ニ+ノ+ハ)で 1/4。
• 回答者が（Ａ）を選ぶ確率は(イ+ウ+シ+ト)/(イ+ウ+カ+ク+シ+ス+ソ+タ+ト+ニ+ノ+ハ)で 1/3。
• 司会者が（Ｂ）からカードを抜いて回答者に示す確率は(イ+ク+ト+ハ)/(イ+ウ+カ+ク+シ+ス+ソ+タ+ト+ニ+ノ+ハ)で 3/8。
• 回答者が（Ａ）を選んだ後に司会者が（Ｂ）からカードを抜いて回答者に示す確率は(イ+ト)/(イ+ウ+シ+ト)で 5/8。
• 回答者が（Ａ）を選んだ後に司会者が（Ｃ）からカードを抜いて回答者に示す確率は(ウ+シ)/(イ+ウ+シ+ト)で 3/8。
• 回答者が（Ａ）を選んだ後に司会者が（Ｂ）からカードを抜いて回答者に示した場合に、（Ａ）が当たりである確率（変形３囚人問題と同様）は(イ)/(イ+ト)で 1/5。
• 回答者が（Ａ）を選んだ後に司会者が（Ｃ）からカードを抜いて回答者に示した場合に、（Ａ）が当たりである確率は(ウ)/(ウ+シ)で 1/3。
• 回答者が（Ａ）を選んだ後に司会者が（Ｂ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、（Ａ）が当たりである確率は(イ+ウ)/(イ+ウ+シ+ト)で 1/4。

　もしも回答者の選択した封筒（Ａ）に当たりのカードが入っている確率を求めるのならば、図のイ、ウ、シ、トの中で考える。「回答者が最初に選択した封筒は（Ａ）」と確定しているからである。もしも回答者が当たりのカードの入っている封筒（Ａ）を選択した確率を求めるのならば、図のイ、ウ、カ、クの中で考える。「当たりのカードの入っている封筒は（Ａ）」と確定しているからである。前者で確率を求める場合は、各封筒に当たりのカードが入っている確率が答に大きく影響するのに対して、後者で確率を求める場合は、各封筒に当たりのカードが入っている確率は答に影響しなくなる。
　例えば、この問題のように封筒（Ｃ）に当たりのカードが入っている確率が 1/2 なら、回答者の選択した封筒（Ａ）に当たりのカードが入っている確率は(イ+ウ)/(イ+ウ+シ+ト)で 1/4 になるが、もしもカードが３枚で封筒（Ｃ）に当たりのカードが入っている確率が 1/3 ならば、回答者の選択した封筒（Ａ）に当たりのカードが入っている確率は同じ計算方法(イ+ウ)/(イ+ウ+シ+ト)でも 1/3 になる。分かりにくい場合は図を書き換えて（【モンティ・ホール問題の解法】に載せてある）確認してほしい。それに対し、封筒（Ｃ）に当たりのカードが入っている確率が 1/2 でも 1/3 でも、回答者が当たりのカードの入っている封筒（Ａ）を選択する確率は(イ+ウ)/(イ+ウ+カ+ク)で 1/3 である。
　同様に、封筒（Ｃ）に当たりのカードが入っている確率が 1/2 の場合、次のようになる。

• 回答者の選択した封筒（Ａ）に当たりのカードが入っている確率は(イ+ウ)/(イ+ウ+シ+ト)で 1/4。
• 回答者の選択した封筒（Ｂ）に当たりのカードが入っている確率は(ス+ソ)/(カ+ス+ソ+ニ)で 1/4。
• 回答者の選択した封筒（Ｃ）に当たりのカードが入っている確率は(ノ+ハ)/(ク+タ+ノ+ハ)で 1/2。
• 回答者が当たりのカードの入っている封筒（Ａ）を選択する確率は(イ+ト)/(イ+ウ+カ+ク)で 1/3。
• 回答者が当たりのカードの入っている封筒（Ｂ）を選択する確率は(ス+ソ)/(シ+ス+ソ+タ)で 1/3。
• 回答者が当たりのカードの入っている封筒（Ｃ）を選択する確率は(ノ+ハ)/(ト+ニ+ノ+ハ)で 1/3。

　封筒（Ｃ）に当たりのカードが入っている確率が 1/3 なら、次のようになる。

• 回答者の選択した封筒（Ａ）に当たりのカードが入っている確率は(イ+ウ)/(イ+ウ+シ+ト)で 1/3。
• 回答者の選択した封筒（Ｂ）に当たりのカードが入っている確率は(ス+ソ)/(カ+ス+ソ+ニ)で 1/3。
• 回答者の選択した封筒（Ｃ）に当たりのカードが入っている確率は(ノ+ハ)/(ク+タ+ノ+ハ)で 1/3。
• 回答者が当たりのカードの入っている封筒（Ａ）を選択する確率は(イ+ト)/(イ+ウ+カ+ク)で 1/3。
• 回答者が当たりのカードの入っている封筒（Ｂ）を選択する確率は(ス+ソ)/(シ+ス+ソ+タ)で 1/3。
• 回答者が当たりのカードの入っている封筒（Ｃ）を選択する確率は(ノ+ハ)/(ト+ニ+ノ+ハ)で 1/3。

　さて、司会者が（Ｂ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。回答者が最初に選択した封筒は（Ａ）とは限らないし、当たりのカードが入っている封筒も（Ａ）とは限らない。同様に司会者が（Ｃ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。司会者が（Ａ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。司会者が（Ｂ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。司会者が（Ａ）か（Ｂ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。司会者が（Ａ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。司会者が（Ａ）か（Ｂ）か（Ｃ）の一枚からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率はどうなるだろうか。
　上の図を使って求めると次のようになる。

• 司会者が（Ｂ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(イ+ハ)/(イ+ク+ト+ハ)で 1/3。
• 司会者が（Ｃ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(ウ+ソ)/(ウ+カ+シ+ソ)で 1/3。
• 司会者が（Ａ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(ス+ノ)/(ス+タ+ニ+ノ)で 1/3。
• 司会者が（Ｂ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(イ+ウ+ソ+ハ)/(イ+ウ+カ+ク+シ+ソ+ト+ハ)で 1/3。
• 司会者が（Ａ）か（Ｂ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(イ+ス+ノ+ハ)/(イ+ク+ス+タ+ト+ニ+ノ+ハ)で 1/3。
• 司会者が（Ａ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(ウ+ス+ソ+ノ)/(ウ+カ+シ+ス+ソ+タ+ニ+ノ)で 1/3。
• 司会者が（Ａ）か（Ｂ）か（Ｃ）の一枚からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率は(イ+ウ+ス+ソ+ノ+ハ)/(イ+ウ+カ+ク+シ+ス+ソ+タ+ト+ニ+ノ+ハ)で 1/3。

　どの確率も 1/3 になった。これはどういうことだろうか。以下に述べるように、同じ 1/3 でも解法が異なり、仮定を変えることで確率が変わるので、偶然の一致と言って良いだろう。

　最後の「司会者が（Ａ）か（Ｂ）か（Ｃ）の一枚からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」は（Ａ）か（Ｂ）か（Ｃ）の一枚がハズレであることは最初から分かっていて司会者がハズレの封筒を示しても新たな情報がないので、最初に回答者が当たりの封筒を選択する確率 1/3 から変化しないということである。「司会者が（Ａ）か（Ｂ）か（Ｃ）の一枚からカードを抜いて回答者に示した場合」というのは、上の図では１周360度全ての場合に相当するので、「司会者がハズレの封筒を示す前に回答者が当たりの封筒を選択する確率」を計算しているだけである。
　ちなみに、最初の選択で回答者が当たりのカードが入った封筒を選択する確率は、封筒（Ａ）、（Ｂ）、（Ｃ）に当たりのカードが入っている確率をそれぞれP(A)、P(B)、P(C)として、回答者が封筒（Ａ）、（Ｂ）、（Ｃ）を選択する確率をそれぞれP(a)、P(b)、P(c)とすると、次のどちらかの数式で求める。

• P(A)P(a|A) + P(B)P(b|B) + P(C)P(c|C)
• P(a)P(A|a) + P(b)P(B|b) + P(c)P(C|c)

　「P(a|A)=P(b|B)=P(c|C)=P(a)=P(b)=P(c)=1/3」（各封筒に当たりのカードが入っている確率が何であれ、どの封筒が高確率か分からない回答者が各封筒を選ぶ確率は同じ）で「P(A)+P(B)+P(C)=1」だから、前者で計算すると容易に 1/3 であることが分かる。後者で計算する場合は「P(A|a)=P(A)」「P(B|b)=P(B)」「P(C|c)=P(C)」（回答者がどの封筒を選択した状態でも各封筒に当たりのカードが入っている確率は変わらない）ことに注目すると容易に 1/3 であることが分かる。

　「司会者が（Ｂ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」が 1/3 になったのは、「イ」と「ウ」の比を「１：１」と仮定して、しかも「ノ」と「ハ」の比も「２：２＝１：１」と仮定しているため、「イ：ク＝ハ：ト＝１：２」になっているからである。
　封筒（Ａ）に当たりのカードが入っていて回答者が封筒（Ａ）を選んだ場合、（Ｂ）も（Ｃ）もハズレで司会者はどちらからカードを抜いてハズレであることを示しても良い。この比を「１：１」にしたのである。【モンティ・ホール問題：補足２】で紹介したように、司会者が「回答者が当たりの封筒（Ａ）を選んだ場合には（Ｃ）からカードを一枚抜いてハズレであることを示す」と決めていた場合、「イ」の領域が「ウ」に占領されて、「司会者が（Ｂ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」は 1/4 に下がる。逆に司会者が「回答者が当たりの封筒（Ａ）を選んだ場合には（Ｂ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ウ」の領域が「イ」に占領されて、確率は 2/5 に上がる。
　さらに、司会者が「回答者が当たりの封筒（Ｃ）を選んだ場合には（Ａ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ハ」の領域が「ノ」に占領されて、確率は 1/7 に下がり、司会者が「回答者が当たりの封筒（Ｃ）を選んだ場合には（Ｂ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ノ」の領域が「ハ」に占領されて、確率は 5/11 に上がる。
　「回答者が当たりの封筒（Ａ）を選んだ場合」にカードを抜く封筒と「回答者が当たりの封筒（Ｃ）を選んだ場合」にカードを抜く封筒の両方を司会者があらかじめ決めていたとしたら、確率はさらに違ったものになる。ここでは省略する。
　「司会者が（Ｃ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」と「司会者が（Ａ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」も同様である。

　しかし、【モンティ・ホール問題：補足２】で解説したケースのように、このゲームでは回答者は司会者がどの封筒からカードを抜いたのは分からない。そこで「司会者が（Ａ）からカードを抜いて回答者に示した場合」と「司会者が（Ｂ）からカードを抜いて回答者に示した場合」と「司会者が（Ｃ）からカードを抜いて回答者に示した場合」の全てのケースを合計して（単に各確率の計算値の値を足すだけではないので注意が必要）確率を求めるのだが、【モンティ・ホール問題：補足２】の最後に計算した結果のように、数式が整理されて「最初の選択で回答者が当たりのカードが入った封筒を選択する確率」（1/3）になる。

　 P("-A"){P(A∩a|"-A")+P(B∩b|"-A")+P(C∩c|"-A")} + P("-B"){P(A∩a|"-B")+P(B∩b|"-B")+P(C∩c|"-B")} + P("-C"){P(A∩a|"-C")+P(B∩b|"-C")+P(C∩c|"-C")}
＝ {P("-A")P(A∩a|"-A")+P("-B")P(A∩a|"-B")+P("-C")P(A∩a|"-C")} + {P("-A")P(B∩b|"-A")+P("-B")P(B∩b|"-B")+P("-C")P(B∩b|"-C")} + {P("-A")P(C∩c|"-A")+P("-B")P(C∩c|"-B")+P("-C")P(C∩c|"-C")}
＝ {P(A∩a)P("-A"|A∩a)+P(A∩a)P("-B"|A∩a)+P(A∩a)P("-C"|A∩a)} + {P(B∩b)P("-A"|B∩b)+P(B∩b)P("-B"|B∩b)+P(B∩b)P("-C"|B∩b)} + {P(C∩c)P("-A"|C∩c)+P(C∩c)P("-B"|C∩c)+P(C∩c)P("-C"|C∩c)}
＝ P(A∩a){P("-A"|A∩a)+P("-B"|A∩a)+P("-C"|A∩a)} + P(B∩b){P("-A"|B∩b)+P("-B"|B∩b)+P("-C"|B∩b)} + P(C∩c){P("-A"|C∩c)+P("-B"|C∩c)+P("-C"|C∩c)}
＝ P(A∩a)+P(B∩b)+P(C∩c)
＝ P(A)P(a|A) + P(B)P(b|B) + P(C)P(c|C)
＝ 1/3

　「司会者が（Ｂ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」はややこしい。とりあえず、1/3 以外の確率になることがあり得るか探してみる。
　「司会者が（Ｂ）からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」と同様に、司会者が「回答者が当たりの封筒（Ａ）を選んだ場合に（Ｂ）と（Ｃ）のどちらからカードを抜いてハズレであることを示すか」を決めていても確率は 1/3 で変わらない。
　しかし、司会者が「回答者が当たりの封筒（Ｂ）を選んだ場合には（Ａ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ソ」の領域が「ス」に占領されて、確率は 2/7 に下がり、逆に司会者が「回答者が当たりの封筒（Ｂ）を選んだ場合には（Ｃ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ス」の領域が「ソ」に占領されて、確率は 3/8 に上がる。
　さらに、司会者が「回答者が当たりの封筒（Ｃ）を選んだ場合には（Ａ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ハ」の領域が「ノ」に占領されて、確率は 3/13 に下がり、司会者が「回答者が当たりの封筒（Ｃ）を選んだ場合には（Ｂ）からカードを一枚抜いてハズレであることを示す」と決めていた場合は「ノ」の領域が「ハ」に占領されて、確率は 7/17 に上がる。
　「回答者が当たりの封筒（Ｂ）を選んだ場合」にカードを抜く封筒と「回答者が当たりの封筒（Ｃ）を選んだ場合」にカードを抜く封筒の両方を司会者があらかじめ決めていたとしたら、確率はさらに違ったものになるが、ここでは省略する。

　「司会者が（Ｂ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」は「司会者が（Ｂ）からカードを抜いて回答者に示した場合」と「司会者が（Ｃ）からカードを抜いて回答者に示した場合」の確率を合計することで求められるのだが、「（Ｂ）か（Ｃ）の一方から」という条件、すなわち「（Ａ）からカードを抜いて回答者に示すことはない」という条件を忘れると間違える。「司会者が（Ａ）か（Ｂ）か（Ｃ）の一枚からカードを抜いて回答者に示した場合」のように足すと間違える。だからややこしい。
　下に数式で表してみるが、上記の円グラフで求めた方が楽である。

　 P("-B"|"-B"∪"-C"){P(A∩a|"-B")+P(B∩b|"-B")+P(C∩c|"-B")} + P("-C"|"-B"∪"-C"){P(A∩a|"-C")+P(B∩b|"-C")+P(C∩c|"-C")}
＝ [P("-B"){P(A∩a|"-B")+P(B∩b|"-B")+P(C∩c|"-B")} + P("-C"){P(A∩a|"-C")+P(B∩b|"-C")+P(C∩c|"-C")}] / P("-B"∪"-C")
＝ [{P("-B")P(A∩a|"-B")+P("-C")P(A∩a|"-C")}+{P("-B")P(B∩b|"-B")+P("-C")P(B∩b|"-C")} + {P("-C")P(C∩c|"-C")+P("-B")P(C∩c|"-B")}] / P("-B"∪"-C")
＝ [{P(A∩a)P("-B"|A∩a)+P(A∩a)P("-C"|A∩a)}+{P(B∩b)P("-B"|B∩b)+P(B∩b)P("-C"|B∩b)} + {P(C∩c)P("-C"|C∩c)+P(C∩c)P("-B"|C∩c)}] / P("-B"∪"-C")
＝ [P(A∩a){P("-B"|A∩a)+P("-C"|A∩a)}+P(B∩b){P("-B"|B∩b)+P("-C"|B∩b)} + P(C∩c){P("-C"|C∩c)+P("-B"|C∩c)}] / P("-B"∪"-C")
＝ [P(A∩a){1-P("-A"|A∩a)}+P(B∩b){1-P("-A"|B∩b)} + P(C∩c){1-P("-A"|C∩c)}] / [1-P("-A")]
＝ [{P(A∩a)+P(B∩b)+P(C∩c)} - {P(A∩a)P("-A"|A∩a)+P(B∩b)P("-A"|B∩b)+P(C∩c)P("-A"|C∩c)}] / [1-P("-A")]
＝ [{P(A∩a)+P(B∩b)+P(C∩c)} - {P((A∩a)∩"-A")+P((B∩b)∩"-A")+P((C∩c)∩"-A")}] / [1-P("-A")]
＝ [{(イ+ウ)+(ス+ソ)+(ノ+ハ)} - {0+ス+ノ}] / [イ+ウ+カ+ク+シ+ソ+ト+ハ]
＝ [イ+ウ+ソ+ハ] / [イ+ウ+カ+ク+シ+ソ+ト+ハ]

　「司会者が（Ａ）か（Ｂ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」と「司会者が（Ａ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」も「司会者が（Ｂ）か（Ｃ）の一方からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」と同じように考えることができる。

　さて、ここまでごちゃごちゃと書いてきたが、途中で書いたとおり、このゲームでは回答者は司会者がどの封筒からカードを抜いたのは分からない。しかも、回答者は自分が選んだ封筒が（Ａ）、（Ｂ）、（Ｃ）のどれであるかも分からない。だから、結局は、「司会者が（Ａ）か（Ｂ）か（Ｃ）の一枚からカードを抜いて回答者に示した場合に、回答者が最初に選択した封筒が当たりである確率」で判断するしかなく、それは上記の通り、「最初の選択で回答者が当たりのカードが入った封筒を選択する確率」である。
　ただ、司会者が１枚の封筒からカードを出した後に、「この封筒は（Ａ）です」などと回答者に情報を提供したら、その情報を使って確率を計算し直した方が良い。さらに、カードの数を変えて、各封筒に当たりのカードが入っている確率が変わると、再選択時に最初の選択のままの方が良い場合があるかもしれない。興味のある方は、いろいろと応用してみてほしい。

タグ：モンティ・ホール問題 ３囚人問題 ベイズの定理 確率 認知心理学