モンティ・ホール問題：プレーヤーが選択する前

　ここでは、モンティ・ホール問題のシミュレーションとして紹介されている【Flash：モンティ･ホール問題: ガスコン研究所】と【ニートが頑張るブログ　 モンティ・ホール問題フラッシュ】のフラッシュの結果について考察する。

　モンティ・ホール問題については何度も書いてきたが（参照）、【モンティ・ホール問題の解法】のようにベイズの定理を使って解く方法が中心だった。それは３囚人問題や変形３囚人問題（参照）と同型だと判断したからである。しかし【モンティ・ホール問題：補足】の頃に本当にベイズの定理を使って解いて良いのか、ベイズ解が正解なのかという疑問が生じた。
　【モンティ・ホール問題：補足】では、プレーヤーがＡのドアを選んだ後に司会者がＢまたはＣのドアを開ける前の状態では、Ｂが開いた場合とＣが開いた場合の両方を加重平均せねばならず、その結果、「選択を変えずに当たる確率」はプレーヤーがドアを選ぶ前から決まっていた「Ａのドアが当たりの確率（P(A)）」と同じになり、「選択を変えて当たる確率」は「Ａ以外のドアが当たりの確率（P(B)+P(C)）」と同じになることを示した。
　また【モンティ・ホール問題：補足３】では、プレーヤーがＡのドアを選んだ後に司会者がＢまたはＣのドアを開ける前の状態では、ＢやＣのドアが当たりである確率もプレーヤーがドアを選ぶ前から変わってないことを示した。
　これらは全て、プレーヤーがドアを選んだ後のことで、プレーヤーがどのドアを選んでも傾向は変わらないとみなしていた。【モンティ・ホール問題の解法】ではプレーヤーが選ぶドアも含めて場合分けして考察しているが、最初にどのドアを選択しても同じ結果（ベイズ解）になることが示されている。実は、【三囚人問題と変形三囚人問題】の「追記（2006/9/9）」に次のような図へリンクしておいた。

（クリックで拡大）

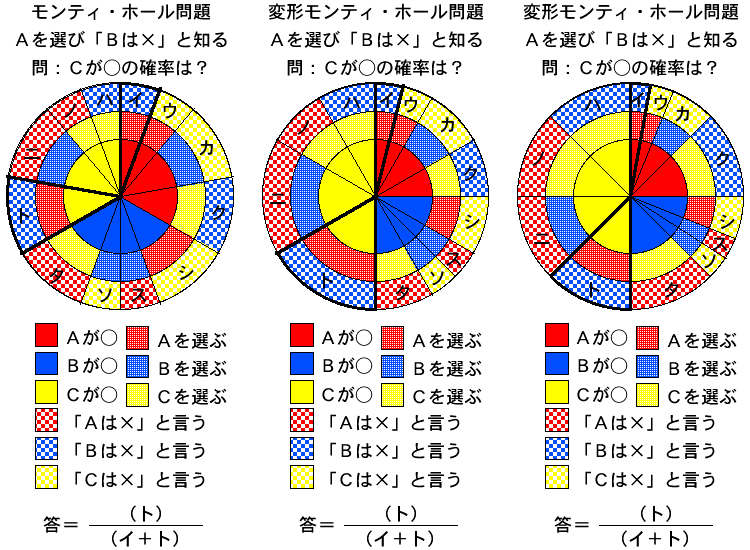
　この円グラフは一周で「確率＝１」である。一番内側の円はＡ，Ｂ，Ｃの各ドアが当たりである確率（P(A),P(B),P(C)）、その外側の円はプレーヤーが各ドアを選択する確率（P(sA),P(sB),P(sC)）、一番外側の円は司会者が各ドアを開く確率（P("-A"),P("-B"),P("-C")）を表している。
　一番左側（以下では「ケース１」と書く）の図は一般的なモンティ・ホール問題を解くための円グラフで各確率は次のようになっている。

1. P(A)=P(B)=P(C)=1/3
2. P(sA|A)=P(sB|A)=P(sC|A)=1/3
3. P(sA|B)=P(sB|B)=P(sC|B)=1/3
4. P(sA|C)=P(sB|C)=P(sC|C)=1/3
5. P("-B"|sA,A)=P("-C"|sA,A)=1/2
6. P("-A"|sB,B)=P("-C"|sB,B)=1/2
7. P("-A"|sC,C)=P("-B"|sC,C)=1/2

　中央（以下では「ケース２」と書く）の図は変形３囚人問題に似せた変形モンティ・ホール問題を解くための円グラフで各確率は次のようになっている。

1. P(A)=P(B)=1/4, P(C)=1/2
2. P(sA|A)=P(sB|A)=P(sC|A)=1/3
3. P(sA|B)=P(sB|B)=P(sC|B)=1/3
4. P(sA|C)=P(sB|C)=P(sC|C)=1/3
5. P("-B"|sA,A)=P("-C"|sA,A)=1/2
6. P("-A"|sB,B)=P("-C"|sB,B)=1/2
7. P("-A"|sC,C)=P("-B"|sC,C)=1/2

　一番右側（以下では「ケース３」と書く）の図は変形３囚人問題に似せた変形モンティ・ホール問題を解くための円グラフでケース２と似ているが、プレーヤーが各ドアを選択する確率を変えてあり、各確率は次のようになっている。

1. P(A)=P(B)=1/4, P(C)=1/2
2. P(sA|A)=P(sB|A)=1/4, P(sC|A)=1/2
3. P(sA|B)=P(sB|B)=1/4, P(sC|B)=1/2
4. P(sA|C)=P(sB|C)=1/4, P(sC|C)=1/2
5. P("-B"|sA,A)=P("-C"|sA,A)=1/2
6. P("-A"|sB,B)=P("-C"|sB,B)=1/2
7. P("-A"|sC,C)=P("-B"|sC,C)=1/2

　ケース１の図を見れば分かるとおり、プレーヤーが最初にどのドアを選択しても、司会者がドアを開いた後に「選択を変えずに当たる確率」（最初に選んだドアが当たりである確率）は1/3に、「選択を変えて当たる確率」（最初に選んだドアがハズレである確率）は2/3になる。グラフでは面積（角度）の割合で直感的に分かるが、通常はどちらもベイズの定理を使って解く。ケース２の図でも、「プレーヤーがＡを選んで司会者がＢのドアを開けた後の選択を変えずに当たる確率」など司会者がドアを開けた後の「選択を変えずに当たる確率」や「選択を変えて当たる確率」がベイズ解と一致することが分かる。ケース３のようにプレーヤが各ドアを選択する確率を変えてもベイズ解と一致する。
　そのことが分かったので、これまではプレーヤーが最初に選ぶドアについては重視してなかった。
　しかし、ケース２やケース３では、プレーヤーが最初に選ぶドアによって「選択を変えずに当たる確率」や「選択を変えて当たる確率」は異なる。ベイズの定理で解けることは一致するが、解が異なる。

　それでは、最初にプレーヤがドアを選択する前の「選択を変えずに当たる確率」や「選択を変えて当たる確率」はどのように計算したら良いだろうか。実は、【Flash：モンティ･ホール問題: ガスコン研究所】や【ニートが頑張るブログ　 モンティ・ホール問題フラッシュ】で提供されている自動計算のシミュレーションはプレーヤーが最初に選ぶドアが確定していない。最初に選ばれるドアが確定していない。おそらく1/3の確率で各ドアが選ばれるようになっているだろう。他のサイトで提供されているシミュレーションも同じではないだろうか。それらのシミュレーションを久しぶりに見て、最初に選ばれるドアが確定してない状態でベイズの定理を使って解くことが妥当だろうかという疑問が生じた。
　結論を先に書くと、最初に選ばれるドアが確定してない状態では「選択を変えずに当たる確率」と「選択を変えて当たる確率」は次の式のようになる。

• 選択を変えずに当たる確率
  = P(sA)P(A) + P(sB)P(B) + P(sC)P(C)
• 選択を変えて当たる確率
  = P(sA)(P(B)+P(C)) + P(sB)(P(A)+P(C)) + P(sC)(P(A)+P(B))

　この式が導かれる過程は私のブログにコメントしてくれたドラザキッドさんがメモで示してくれた（参照）。ただし、私のブログでは各確率の記号を変えた。
　プレーヤーが各ドアを選択する確率（P(sA),P(sB),P(sC)）で、それぞれのドアが選ばれた場合の「選択を変えずに当たる確率」（例えばプレーヤがＡを選んだらP(A)）や「選択を変えて当たる確率」（例えばプレーヤーがＡを選んだらP(B)+P(C)）を加重平均した形になっている。それぞれのドアが選ばれた場合の「選択を変えずに当たる確率」や「選択を変えて当たる確率」は司会者がドアを開ける前の確率なので、【モンティ・ホール問題：補足】で書いたように、各ドアが開いた後のベイズ解を加重平均して求められ、「選択を変えずに当たる確率」は事前確率（各ドアが当たりである確率（P(A),P(B),P(C)））と同じになる。
　ドラザキッドさんのメモにも書いてあるが、「P(sA)=P(sB)=P(sC)=1/3」では、P(A),P(B),P(C)がどんな値でも、「選択を変えずに当たる確率」は1/3になり、「選択を変えて当たる確率」は2/3になる。これが各サイトで提供されているシミュレーションの結果だろう。事前確率を変えても結果が変わらないシミュレーションである。ベイズの定理を使って解くことに意味が見出せない。
　また、通常のモンティ・ホール問題のように「P(A)=P(B)=P(C)=1/3」ならばP(sA),P(sB),P(sC)がどんな値でも、「選択を変えずに当たる確率」は1/3になり、「選択を変えて当たる確率」は2/3になる。

　上記のケース１、ケース２、ケース３の円グラフでは次のように各領域の和になる。

• 選択を変えずに当たる確率
  =（イ＋ウ）＋（ス＋ソ）＋（ノ＋ハ）
• 選択を変えて当たる確率
  =（カ＋ク）＋（シ＋タ）＋（ト＋ニ）

　ケース１、ケース２では、「選択を変えずに当たる確率」は1/3になり「選択を変えて当たる確率」は2/3になっていることが分かる。ケース２ではケース１と事前確率（各ドアが当たりである確率（P(A),P(B),P(C)））が異なるのに同じ結果になっている。
　ケース３では、「選択を変えずに当たる確率」は3/8で、「選択を変えて当たる確率」は5/8である。これは、事前確率ともベイズ解とも異なる。プレーヤーが最初に選ぶドアに偏りがあった結果である。

　ここで、少し注意が必要なので言及しておく。
　上記のケース１、ケース２、ケース３の全てで次の式が成立している。

1. P(sA|A)=P(sA|B)=P(sA|C)
2. P(sB|A)=P(sB|B)=P(sB|C)
3. P(sC|A)=P(sC|B)=P(sC|C)

　この式から次の式が成立する。

1. P(sA)=P(sA|A)=P(sA|B)=P(sA|C)
2. P(sB)=P(sB|A)=P(sB|B)=P(sB|C)
3. P(sC)=P(sC|A)=P(sC|B)=P(sC|C)

　この仮定は妥当だと思うが、妥当でないのならば、もう少し詳細な考察が必要だろう。

　ところで、以上のことを確認するためのExcelファイルを作った。

• MontyHall_2.xls

　プレーヤーが最初に選ぶドアを固定して考察するのなら以前のバージョン（MontyHall.xls）の方が使いやすい。

　MontyHall_2.xls では「ドア」を「箱」に置き換えてある。
　各箱が当たりである確率（P(A),P(B),P(C)）は箱に入れる玉の数（セルD8,D9,D10）で調整する。
　プレーヤーが各箱を最初に選択する確率（P(sA),P(sB),P(sC)）は「プレーヤーの選択」と書いてある枠の所（セルC18,C19,C20）で変える。例えば「プレーヤーが最初に選択する箱はＡ」と決めてシミュレーションする場合は、P(sA)に相当するＡの右（セルC18）を1にして他を0にする。
　プレーヤが箱を選んだ後に司会者が各箱を開ける確率（P("-B"|sA,A),P("-A"|sB,B),P("-A"|sC,C)）は「司会者の開ける確率」と書いてある枠の所（セルH9,L8,P8）で変える。P("-C"|sA,A),P("-C"|sB,B),P("-B"|sC,C)は自動的に計算される（セルH10,L10,P9）。
　「司会者の開ける確率」枠の一番右側の「A∪B∪C」列は各箱が開く確率であり、次の式に相当する。

1. P("-A") = P(B)*P(sB)*P("-A"|sB,B) + P(C)*P(sB)*P("-A"|sB,C) + P(B)*P(sC)*P("-A"|sC,B) + P(C)*P(sC)*P("-A"|sC,C)
2. P("-B") = P(A)*P(sA)*P("-B"|sA,A) + P(C)*P(sA)*P("-B"|sA,C) + P(A)*P(sC)*P("-B"|sC,A) + P(C)*P(sC)*P("-B"|sC,C)
3. P("-C") = P(A)*P(sA)*P("-C"|sA,A) + P(B)*P(sA)*P("-C"|sA,B) + P(A)*P(sB)*P("-C"|sB,A) + P(B)*P(sB)*P("-C"|sB,B)

　「再選択率」の枠（セルD14）は司会者が箱を開けた後に選択を変える確率を設定する。通常は0.5であるが、「変更する」と決めてシミュレーションする場合は1にして、「変更しない」と決めてシミュレーションする場合は0にする。
　シミュレーション結果の「当たり？」の列（J列）はプレーヤーが最終的に選んだ箱が当たりである場合は○で表示してハズレである場合は×で表示している。
　シミュレーション結果の「A∪B∪Cが開く」の列（K列、L列）は「当たり？」の列（J列）から選択の変更がなかった場合（変更なし）と変更があった場合（変更あり）を抽出している。
　シミュレーション結果の「Aが開いた場合」（M列、N列）「Bが開いた場合」（O列、P列）「Cが開いた場合」（Q列、R列）の列は「A∪B∪Cが開く」の列（K列、L列）から司会者によって各箱が開けられた場合を抽出している。
　「○の数」「×の数」の行（18行、19行）でシミュレーション結果のそれぞれの数をカウントしている。
　「○の率」「×の率」の行（16行、17行）は「○の数」「×の数」の行（18行、19行）の結果を確率に変換していて、「○の率」が当たる確率である。
　「理論値」の行（15行）は下の「○の率」と比較するために用意されていて、次のように計算している。

1. 「Ａが開いた場合」の「変更なし」（セルM15）：
   ( P(B)*P(sB)*P("-A"|sB,B) + P(C)*P(sC)*P("-A"|sC,C) )/P("-A")
2. 「Ａが開いた場合」の「変更あり」（セルN15）：
   ( P(C)*P(sB)*P("-A"|sB,C) + P(B)*P(sC)*P("-A"|sC,B) )/P("-A")
3. 「Ｂが開いた場合」の「変更なし」（セルO15）：
   ( P(A)*P(sA)*("-B"|sA,A) + P(C)*P(sC)*P("-B"|sC,C) )/P("-B")
4. 「Ｂが開いた場合」の「変更あり」（セルP15）：
   ( P(C)*P(sA)*P("-B"|sA,C) + P(A)*P(sC)*P("-B"|sC,A) )/P("-B")
5. 「Ｃが開いた場合」の「変更なし」（セルQ15）：
   ( P(A)*P(sA)*P("-C"|sA,A) + P(B)*P(sB)*P("-C"|sB,B) )/P("-C")
6. 「Ｃが開いた場合」の「変更あり」（セルR15）：
   ( P(B)*P(sA)*P("-C"|sA,B) + P(A)*P(sB)*P("-C"|sB,A) )/P("-C")
7. 「A∪B∪Cが開く」の「変更なし」（セルK15）：
   P("-A")*（セルM15）+ P("-B")*（セルO15）+ P("-C")*（セルQ15）
8. 「A∪B∪Cが開く」の「変更あり」（セルL15）：
   P("-A")*（セルN15）+ P("-B")*（セルP15）+ P("-C")*（セルR15）
9. 「当たり？」の列の理論値（セルJ15）：
   （セルD14）*（セルL15）+(1-（セルD14）)*（セルK15）

　モンティ・ホール問題で多くの人が示している「ドアを変えた場合の確率」は「セルL15」にある理論値（シミュレーション結果は「セルL16」）のことで「ドアを変えない場合の確率」に相当する「セルK15」の理論値（シミュレーション結果は「セルK16」）と比較して大きいと解答している。三囚人問題ではプレーヤーが最初に選ぶ箱を一つに固定して（セルC18,C19,C20で一つを１にして他を０にする）、A,B,Cのどれかが開いた場合の確率（セルM15～R15）を見る。それはベイズ解に一致している。
　この理論値「セルK15」と「セルL15」については「セルK21」と「セルL21」に別の計算式を入力してある。それは、次の式に相当するが、「セルK15」と「セルL15」の値と一致していることが確認できる。

1. 「A∪B∪Cが開く」の「変更なし」（セルK21）：
   P(sA)*P(A) + P(sB)*P(B) + P(sC)*P(C)
2. 「A∪B∪Cが開く」の「変更あり」（セルL21）：
   P(sA)*(P(B)+P(C)) + P(sB)*(P(A)+P(C)) + P(sC)*(P(A)+P(B))

　最後に私のブログでも次の式を導いておく。

• 選択を変えずに当たる確率 = P(sA)P(A) + P(sB)P(B) + P(sC)P(C)
• 選択を変えて当たる確率 = P(sA)(P(B)+P(C)) + P(sB)(P(A)+P(C)) + P(sC)(P(A)+P(B))

選択を変えずに当たる確率

1. 選択を変えずに当たる確率 = P("-B",sA,A) + P("-C",sA,A) + P("-A",sB,B) + P("-C",sB,B) + P("-A",sC,C) + P("-B",sC,C)
2. P("-B",sA,A)=P(A)P(sA|A)P("-B"|sA,A)
3. P("-C",sA,A)=P(A)P(sA|A)P("-C"|sA,A)
4. P("-A",sB,B)=P(B)P(sB|B)P("-A"|sB,B)
5. P("-C",sB,B)=P(B)P(sB|B)P("-C"|sB,B)
6. P("-A",sC,C)=P(C)P(sC|C)P("-A"|sC,C)
7. P("-B",sC,C)=P(C)P(sC|C)P("-B"|sC,C)
8. P("-B",sA,A)+P("-C",sA,A) = P(A)P(sA|A)(P("-B"|sA,A)+P("-C"|sA,A))
9. P("-B",sA,A)+P("-C",sA,A) = P(A)P(sA|A) （∵P("-B"|sA,A)+P("-C"|sA,A)=1）
10. P("-A",sB,B)+P("-C",sB,B) = P(B)P(sB|B)(P("-A"|sB,B)+P("-C"|sB,B))
11. P("-A",sB,B)+P("-C",sB,B) = P(B)P(sB|B) （∵P("-A"|sB,B)+P("-C"|sB,B))=1）
12. P("-A",sC,C)+P("-B",sC,C) = P(C)P(sC|C)(P("-A"|sC,C)+P("-B"|sC,C))
13. P("-A",sC,C)+P("-B",sC,C) = P(C)P(sC|C) （∵P("-A"|sC,C)+P("-B"|sC,C)=1）
14. 選択を変えずに当たる確率 = P(A)P(sA|A) + P(B)P(sB|B) + P(C)P(sC|C)
15. 選択を変えずに当たる確率 = P(A)P(sA) + P(B)P(sB) + P(C)P(sC)

あるいは

1. 選択を変えずに当たる確率 = P("-B",sA,A) + P("-C",sA,A) + P("-A",sB,B) + P("-C",sB,B) + P("-A",sC,C) + P("-B",sC,C)
2. P("-B",sA,A)=P(sA)P(A|sA)P("-B"|sA,A)
3. P("-C",sA,A)=P(sA)P(A|sA)P("-C"|sA,A)
4. P("-A",sB,B)=P(sB)P(B|sB)P("-A"|sB,B)
5. P("-C",sB,B)=P(sB)P(B|sB)P("-C"|sB,B)
6. P("-A",sC,C)=P(sC)P(C|sC)P("-A"|sC,C)
7. P("-B",sC,C)=P(sC)P(C|sC)P("-B"|sC,C)
8. P("-B",sA,A)+P("-C",sA,A) = P(sA)P(sA|A)(P("-B"|sA,A)+P("-C"|sA,A))
9. P("-B",sA,A)+P("-C",sA,A) = P(sA)P(A|sA) （∵P("-B"|sA,A)+P("-C"|sA,A)=1）
10. P("-A",sB,B)+P("-C",sB,B) = P(sB)P(B|sB)(P("-A"|sB,B)+P("-C"|sB,B))
11. P("-A",sB,B)+P("-C",sB,B) = P(sB)P(B|sB) （∵P("-A"|sB,B)+P("-C"|sB,B))=1）
12. P("-A",sC,C)+P("-B",sC,C) = P(sC)P(C|sC)(P("-A"|sC,C)+P("-B"|sC,C))
13. P("-A",sC,C)+P("-B",sC,C) = P(sC)P(C|sC) （∵P("-A"|sC,C)+P("-B"|sC,C)=1）
14. 選択を変えずに当たる確率 = P(sA)P(A|sA) + P(sB)P(B|sB) + P(sC)P(C|sC)
15. 選択を変えずに当たる確率 = P(sA)P(A) + P(sB)P(B) + P(sC)P(C)

選択を変えて当たる確率

1. 選択を変えて当たる確率 = P("-C",sB,A) + P("-B",sC,A) + P("-C",sA,B) + P("-A",sC,B) + P("-B",sA,C) + P("-A",sB,C)
2. P("-C",sB,A)=P(A)P(sB|A)P("-C"|sB,A)=P(A)P(sB|A) （∵P("-C"|sB,A)=1）
3. P("-B",sC,A)=P(A)P(sC|A)P("-B"|sC,A)=P(A)P(sC|A) （∵P("-B"|sC,A)=1）
4. P("-C",sA,B)=P(B)P(sA|B)P("-C"|sA,B)=P(B)P(sA|B) （∵P("-C"|sA,B)=1）
5. P("-A",sC,B)=P(B)P(sC|B)P("-A"|sC,B)=P(B)P(sC|B) （∵P("-A"|sC,B)=1）
6. P("-B",sA,C)=P(C)P(sA|C)P("-B"|sA,C)=P(C)P(sA|C) （∵P("-B"|sA,C)=1）
7. P("-A",sB,C)=P(C)P(sB|C)P("-A"|sB,C)=P(C)P(sB|C) （∵P("-A"|sB,C)=1）
8. 選択を変えて当たる確率 = P(A)(P(sB|A)+P(sC|A)) + P(B)(P(sA|B)+P(sC|B)) + P(C)(P(sA|C)+P(sB|C))
9. 選択を変えて当たる確率 = P(A)(P(sB)+P(sC)) + P(B)(P(sA)+P(sC)) + P(C)(P(sA)+P(sB))
10. 選択を変えて当たる確率 = P(sA)(P(B)+P(C)) + P(sB)(P(A)+P(C)) + P(sC)(P(A)+P(B))

あるいは

1. 選択を変えて当たる確率 = P("-C",sB,A) + P("-B",sC,A) + P("-C",sA,B) + P("-A",sC,B) + P("-B",sA,C) + P("-A",sB,C)
2. P("-C",sB,A)=P(sB)P(A|sB)P("-C"|sB,A)=P(sB)P(A|sB) （∵P("-C"|sB,A)=1）
3. P("-B",sC,A)=P(sC)P(A|sC)P("-B"|sC,A)=P(sC)P(A|sC) （∵P("-B"|sC,A)=1）
4. P("-C",sA,B)=P(sA)P(B|sA)P("-C"|sA,B)=P(sA)P(B|sA) （∵P("-C"|sA,B)=1）
5. P("-A",sC,B)=P(sC)P(B|sC)P("-A"|sC,B)=P(sC)P(B|sC) （∵P("-A"|sC,B)=1）
6. P("-B",sA,C)=P(sA)P(C|sA)P("-B"|sA,C)=P(sA)P(C|sA) （∵P("-B"|sA,C)=1）
7. P("-A",sB,C)=P(sB)P(C|sB)P("-A"|sB,C)=P(sB)P(C|sB) （∵P("-A"|sB,C)=1）
8. 選択を変えて当たる確率 = P(sA)(P(B|sA)+P(C|sA)) + P(sB)(P(A|sB)+P(C|sB)) + P(sC)(P(A|sC)+P(B|sC))
9. 選択を変えて当たる確率 = P(sA)(P(B)+P(C)) + P(sB)(P(A)+P(C)) + P(sC)(P(A)+P(B))

　ここでも注意が必要なので言及しておく。
　ここでは次の式が成立していることを前提にしている。

1. P(sA|A)=P(sA|B)=P(sA|C)=P(sA)
2. P(sB|A)=P(sB|B)=P(sB|C)=P(sB)
3. P(sC|A)=P(sC|B)=P(sC|C)=P(sC)
4. P(A|sA)=P(A|sB)=P(A|sC)=P(A)
5. P(B|sA)=P(B|sB)=P(B|sC)=P(B)
6. P(C|sA)=P(C|sB)=P(C|sC)=P(C)

　この前提は妥当だと思うが、妥当でないのならば、もう少し詳細な考察が必要だろう。

タグ：確率 モンティ・ホール問題 ３囚人問題 ベイズの定理