Ｎドア問題の解法

『モンティ・ホール問題 - Wikipedia』を読んで

　英語版の「Monty Hall problem - Wikipedia, the free encyclopedia」は日本語版のサイトと内容が異なるようだが、私は英語が苦手なので、ここでは日本語版のサイトの方について考察する。

　ここで紹介されているモンティ・ホール問題の解法の問題点ついては前に述べた（参照）。そして、正式な解法と思われるものも前に書いた（参照）。ただ、次の問題の解法については省略した。

また、ドアが3個ではなく100個である場合を考えるとより直感的に分かりやすくなるだろう。プレイヤーが一つのドアを選んだのち、モンティは後ろにヤギのいる98個のドアを開ける。明らかに、モンティが開けなかったもう一つのドアに景品がある可能性が極めて高い（正確には 99/100）。
（「モンティ・ホール問題 - Wikipedia」）

　この問題の解法を次のように「Ｎドア問題」に一般化して述べる。

　Ｎ個のドアがあって、１個のドアの後ろだけ景品があり、残りのドアの後ろにはヤギがいることが分かっている（Ｎ≧３）。景品がある確率はそれぞれP(1)、P(2)、…、P(N)であった。モンティはどのドアの後ろに景品があるか知っているが、プレーヤーは知らない。プレーヤーがドア１を選んだ後、モンティはドア１とドア２を残して他のドアを全て開けた。開けられたすべてのドアの後ろにはヤギがいた。ドア２の後ろに景品がある確率はいくらか？

　正式な解法はベイズの定理を用いる方法だろう。
　モンティがドア２を残した後のドア１とドア２の事後確率P(1|"2")、P(2|"2")を求めれば良い。
　ドア１に景品が入っている時にモンティがドア２を残す確率をP("2"|1)、ドア２に景品が入っている時にモンティがドア２を残す確率をP("2"|2)とする。一般にドアｉ（１≦ｉ≦Ｎ）に景品が入っている時にモンティがドア２を残す確率をP("2"|i)とする。ドアＮに景品が入っている時にモンティがドア２を残す確率はP("2"|N)である。
　するとP(1|"2")とP(2|"2")は次の式（ベイズの定理）で求められる。

　P(1|"2") = P(1)P("2"|1)/(P(1)P("2"|1)+P(2)P("2"|2)+...+P(N)P("2"|N))
　P(2|"2") = P(2)P("2"|2)/(P(1)P("2"|1)+P(2)P("2"|2)+...+P(N)P("2"|N))

　分母はモンティがドア２を残す確率の合計であり、分子はドア１、ドア２が当たりでかつモンティがドア２を残す確率である。
　さて、モンティは景品の入っているドアを開けずドア１以外は１つしかドアを残せないので、ドア１とドア２以外に景品が入っている場合はそのドアを残すはずでドア２を残すことはできない。すなわちｉ≧３では「P("2"|i)=0」である。したがって上の式は次のように簡略化できる。

　P(1|"2") = P(1)P("2"|1)/(P(1)P("2"|1)+P(2)P("2"|2))
　P(2|"2") = P(2)P("2"|2)/(P(1)P("2"|1)+P(2)P("2"|2))

　勉強不足ではっきりとは分からないが、このように簡略化する際に、たぶん「P(i)=0（i≧3）」としてはいけないだろう。P(i)はドア２を残す前の事前確率で、ドア２を残した後の事後確率P(i|"2")ではないからである。「P(i|"2")=0（i≧3）」は結果として正しい。P(i|"2")は式で表すと次のようになる。

　P(i|"2") = P(i)P("2"|i)/(P(1)P("2"|1)+P(2)P("2"|2)+...+P(N)P("2"|N))

　ｉ≧３では分母は「P(1)P("2"|1)+P(2)P("2"|2)」が残るが、分子は「P("2"|i)=0」なので０になり、P(i|"2")は０になる。すなわち「P("2"|i)=0（i≧3）」の結果として「P(i|"2")=0（i≧3）」となる。

　P(1|"2")、P(2|"2")の式に次の値を代入する。と、代入したくてもＮの値などが定まらないと各確率が分からず代入できない。そこで、まずはモンティ・ホール問題（３ドア問題）の値を代入してみる。

　P(1) = P(2) = 1/3
　P("2"|1) = 1/2　（∵ P("2"|1)+P("3"|1)=1、P("2"|1)=P("3"|1)）
　P("2"|2) = 1

　するとP(1|"2")とP(2|"2")は次のようになる。

　P(1|"2") = (1/6)/(1/6 + 1/3) = 1/3
　P(2|"2") = (1/3)/(1/6 + 1/3) = 2/3

　最初に選んだドア１よりも残ったドア２の方が景品の入っている確率が高い。ドアを変えた方が良いということである。

　このように、【モンティ・ホール問題の解法】で紹介したベイズの定理を使う解法（残したドアではなく開けたドアに注目して条件つき確率の条件とした解法）とは違う式（ベイズの定理を使うことは同じ）だが、同じ答になる。

　それでは、「モンティ・ホール問題 - Wikipedia」に載っていたＮ＝１００の場合を計算する。
　P(1|"2")とP(2|"2")は次の式で求められる。

　P(1|"2") = P(1)P("2"|1)/(P(1)P("2"|1)+P(2)P("2"|2))
　P(2|"2") = P(2)P("2"|2)/(P(1)P("2"|1)+P(2)P("2"|2))

　この式に、次の値を代入する。

　P(1) = P(2) = 1/100
　P("2"|1) = 1/99　（∵ P("2"|1)+P("3"|1)+...+P("100"|1)=1、P("2"|1)=...=P("100"|1)）
　P("2"|2) = 1

　するとP(1|"2")とP(2|"2")は次のようになる。

　P(1|"2") = (1/9900)/(1/9900 + 1/100) = 1/100
　P(2|"2") = (1/100)/(1/9900 + 1/100) = 99/100

　圧倒的に、最初に選んだドア１よりも残ったドア２の方が景品の入っている確率が高い。ドアを変えた方が良いということである。

　次に、【モンティ・ホール問題】で紹介した次の問題で計算してみる。

　１００個のドアがあって、１個のドアの後ろだけ景品があり、残りのドアの後ろにはヤギがいることが分かっている。景品がある確率は一つだけ2/101で他は1/101であった。モンティはどのドアの後ろに景品があるか知っているが、プレーヤーは知らない。プレーヤーがドア１（景品のある確率は1/101）を選んだ後、モンティはドア１とドア２（景品がある確率は2/101）を残して他のドアを全て開けた。開けられたすべてのドアの後ろにはヤギがいた。モンティが残したドア２の後ろに景品がある確率はいくらか。

　P(1|"2")とP(2|"2")は次の式で求められる。

　P(1|"2") = P(1)P("2"|1)/(P(1)P("2"|1)+P(2)P("2"|2))
　P(2|"2") = P(2)P("2"|2)/(P(1)P("2"|1)+P(2)P("2"|2))

　この式に、次の値を代入する。

　P(1) = 1/101
　P(2) = 2/101
　P("2"|1) = 1/99　（∵ P("2"|1)+P("3"|1)+...+P("100"|1)=1、P("2"|1)=...=P("100"|1)）
　P("2"|2) = 1

　するとP(1|"2")とP(2|"2")は次のようになる。

　P(1|"2") = (1/9999)/(1/9999 + 2/101) = 1/199
　P(2|"2") = (2/101)/(1/9999 + 2/101) = 198/199

　「P(2|"2")=(1-1/101)=100/101」ではない。

　ちなみに、プレーヤーがドア１を選ぶ前のドア２の後ろに景品がある事前確率が1/101だった（確率2/101のドアは開けられてしまった）ら、次の値を代入する。

　P(1) = 1/101
　P(2) = 1/101
　P("2"|1) = 1/99　（∵ P("2"|1)+P("3"|1)+...+P("100"|1)=1、P("2"|1)=...=P("100"|1)）
　P("2"|2) = 1

　するとP(1|"2")とP(2|"2")は次のようになる。

　P(1|"2") = (1/9999)/(1/9999 + 1/101) = 1/100
　P(2|"2") = (1/101)/(1/9999 + 1/101) = 99/100

　「P(2|"2")=(1-1/101)=100/101」ではない。

　また、プレーヤが選んだドア１の後ろに景品がある事前確率が2/101だったら、次の値を代入する。

　P(1) = 2/101
　P(2) = 1/101
　P("2"|1) = 1/99　（∵ P("2"|1)+P("3"|1)+...+P("100"|1)=1、P("2"|1)=...=P("100"|1)）
　P("2"|2) = 1

　するとP(1|"2")とP(2|"2")は次のようになる。

　P(1|"2") = (2/9999)/(2/9999 + 1/101) = 2/101
　P(2|"2") = (1/101)/(2/9999 + 1/101) = 99/101

　「P(1|"2")=P(1)、∴ P(2|"2")=(1-P(1|"2"))=(1-2/101)=99/101」という解法と同じ答だが、考え方が全く異なる。
　「P(1|"2")=P(1)」として解くことができる条件については【モンティ・ホール問題】で述べた。その条件は「P("2"|1) = P(2)/(1-P(1))」である。

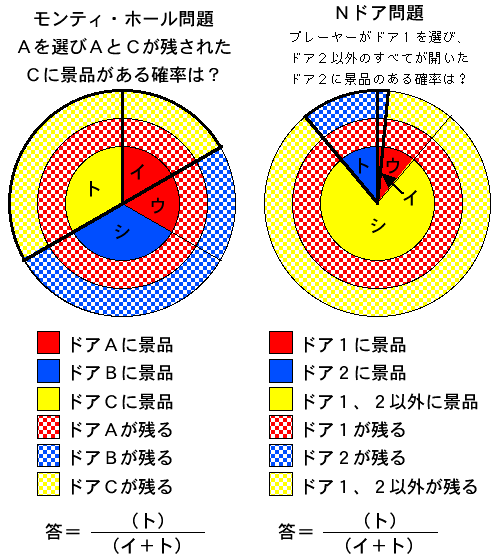
　さて、Ｎドア問題の解法を円グラフを用いた図（参照）で表現すると次のようになる。代表としてモンティ・ホール問題（３ドア問題）も一緒に示した。

　１周（３６０度）が確率１であり、各ケースで分け合い、「扇の角度÷３６０」が各ケースの確率になる。角度の比が確率の比である。内側が事前確率で外側に行くに連れて場合分けされている。樹形図の枝別れに相当する。「P(1|"2")=P(1)」として解くことができる条件は「イ／（イ＋ウ）＝ト／（ト＋シ）」である。その条件を満たさない場合は今回の記事のようにベイズの定理を使って解く必要がある。Ｎドア問題も場合分けして条件つき確率を求めることで解くことができるだろうが、面倒なので省略する。

---

　モンティ・ホール問題で「プレーヤーが選ばなかった複数のドアの一つがハズレであることを知ってもプレーヤーが選んだドアが当たりである確率は変わらない。プレーヤーが選ばなかった２つのドアは１つにまとめて考えることができて、その合計確率は変わらないのだから、一方の確率が０になったらもう一方の確率はその合計確率になる」という画期的な解法があることを知って即座に納得し、すぐに変形三囚人問題に応用してみたら同じ解法が使えないことを知り、変形三囚人問題に応用する方法はないものかと探したが見つからず、画期的だと思った解法が間違っているのではないかと思い間違い探しを始め、参考文献(2)を読んで何となく問題点らしきもの（「不変の定理」という主観的定理）を見つけ、その問題点が問題であることを示して納得してもらえる方法を探して、今日に至った。長かった。疲れた。結局、簡単な文章で問題点を指摘することはできなかったが、かなり勉強になった。参考文献(2)はかなり前に読んでいたのだが、改めて読んだら前よりも頭に入った。一段落ついて改めて他のサイトを見てみたら、正式な解法を載せているサイトが多数あった。「不変の定理」の間違いに気付いているサイトもあったような気がする。ベイズの定理や変形三囚人問題に触れているサイトにその傾向があった。私のブログに書く必要はなかったかなぁ、と思うが、書いちゃったのでそのままにする。
　モンティ・ホール問題に関する考察は、とりあえずこれで終わりにしたい。ベイズの定理に関しては「少数事例において専門家の意見が正しい確率」という観点で少し思うところがあるので、気が向いたら書くかもしれない。とにかく、これで一段落。

---

参考文献
(1)「考えることの科学〜推論の認知心理学への招待〜」（市川伸一著、中公新書）
(2)「確率の理解を探る〜３囚人問題とその周辺〜」（市川伸一著、共立出版）

---

これまでの「三囚人問題、モンティ・ホール問題（モンティ・ホール・ジレンマ）」関連記事

【三つの扉、三枚の封筒】
【三囚人問題の図解】
【変形三択問題】
【三囚人問題と変形三囚人問題】
【金の玉はどこだ！問題】
【モンティ・ホール問題】
【モンティ・ホール問題の解法】

続きの記事

【モンティ・ホール問題：補足】

タグ：モンティ・ホール問題 ３囚人問題 ベイズの定理 確率 認知心理学